Research interests

Shrinkage priors/Scalable Bayes

Shrinkage priors (Polson & Scott, 2010) have been shown to have nice properties in high dimensional problems. They often outperform frquentist regularization methods (Bhattachrya, Chakraborty & Mallick, 2016) and can automatically provide uncertainty quantifications. But standard Markov chain Monte Carlo algorithms to sample from the posterior distribution are very scale as a cubic with the dimension of the parameter limiting the applications of these priors in many applications, for example, in GWAS studies. In Bhattachrya, Chakraborty & Mallick (2016), we propose a novel algorithm to sample from the posterior that scales linearly with the dimension. Although the algorithm is oroginally developed in a high dimensional regression setting, the same principle can be applied in other high dimensional problems such as covariance matrix estimation, factor models, dictionary learning etc. The following image shows the computing time of an algorithm (black solid line) proposed in (Rue, 2001) and that of the proposed algorithm (black dotted line) in logarithmic scale. Clearly, the gains are huge when the dimension (p) increases.

In Chakraborty, Bhattacharya & Mallick (2020) we study relationship between a large number of precitors with several response variables. We extend the traditional reduced rank regression setup to accommodate modern high dimensional data sets by carefully designing shrinkage priors over the parameter space. We also study the behaviour of the posterior distribution in a non-asymptotic setting. En route, we prove a critical prior concentration property of the popular Horseshoe prior. Moreover, we show how the recently developed fractional posterior framework in Bhattacharya, Pati & Yang(2019) can be used to study the operating characteristics of the posterior distribution. The following plot shows the results of our proposed method in an application to Yeast cell cycle data. The plots shows estimated effects of two potential transcription factors regulating cell cycles.

Dirichlet process priors are one of the most popular Bayesian methods for nonparametric density estimation. While researchers have proposed many algorithms for posterior computation, they involve a delicate trade off between good mixing and computation time. Additionally, these methods are not suitable for high dimensional data which lie on lower dimensional manifolds such as data on galaxies, stars etc. In Chattopadhyay, Chakraborty & Dunson (2020+) we propose a pseudo Bayes approach combining the algorithmic simplicity of nearest neighbor methods and statistical versataility of Dirichlet process. The method involves in partititoning the data according to nearest neighborhoods and fitting a kernel, typicallu Gaussian, within each neighborhood. The fixed partitioning results in huge gains in computation time while the final mixture model formulation enables the method to efficiently estimate a wide range of densities. As an aplication we consider classification of pulsar stars from data obtained from the high time resolution universe survey data. This data is publicly available from the UCI machine leraning repository. Our proposed method does a similar job in calibrating the classfication probabilities on held-out sets as the classicial Dirichlet process.

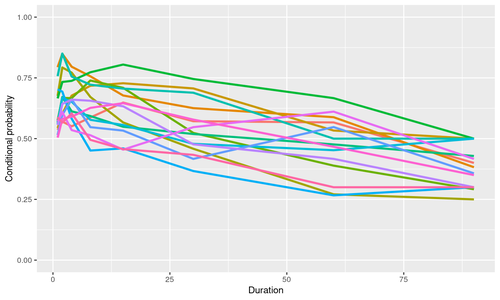
Bird songs play a major role in mate selection and thus have a pronounced impact on their population dynamics. Automated acoustic monitoring is increasingly used in both ecological studies and in conservation. It is thus importat for Ecologists to understand temporal patterns obsrved in bird vocalizations. In Chakraborty, Ovaskainen & Dunson (2020+) we develop a new class model that can potentially explain temporal variations in bird vocalization. The motivation in building these new class of model is to explain the scaling of conditional probabilities in bird vocalizations. From a purely statistical point of view the fact that the data is observed as a sequence of binary variables indicating occurrence/non-occorrence of bird vocalizations presensted a new challenge. The possible presence of long range dependence in this case is aligned with observations made in other naturally occurring events such as earthquakes, avalanches etc. See below for a snapshot of vocalization of one bird species over time and the scaling of conditional probabilities of 15 different bird species.
Recorded data: black bars = 1 (vocaliztion), white bars = 0 (no vocalization)
Scaling of conditional probabilities at different time scales
I am part of the Lifeplan project which aims to map global biodiversity. Apart from its tremendous scientific value the data collected by the scientists pose delightful statistical challenges. You can follow Lifeplan on Twitter.